L可测集和L测度的关系
L可测集和L测度的关系:可测集的构造是依赖外测度的。即满足卡氏条件的集合组成可测集全体。满足可测集的交并条件。比如那个可测集合是E=(0,1)(测度有限),函数是f(x)=1/x可测,那么积分∫_Efdm=+∞,所以f不是Lebesgue可积。先在基本空间x上定义一个测度函数m,这个测度函数的性质,尤其可列可加性“扩大”到让更多的集合满足。

有界点集E
把所有包含E的有界开集的测度的下确界称为E的外测度,记为m*(E),即m*(E)=inf{m(G)|G为开集且G⊃E};把所有包含E的有界开集的测度的上确界称为E的(勒贝格)内测度,记为m*(E)或|E|i,即m*(E)=sup{m(F)|F为闭集且F⊃E};显然,m*(E)≤m*(E);若m*(E)=m*(E),则称E为可测集,它的外测度与内测度所具有的共同值称为E的测度,记为m(E)=m,(E)=m*(E)。
举例说明什么是勒贝格测度
举例来说,如果A是一个区间[a,b],那么其勒贝格测度是区间长度b-a。开区间(a,b)的长度与闭区间一样,因为两集合的差是零测集。如果A是区间[a,b]和[c,d]的笛卡尔积,则它是一个长方形,测度为它的面积(b-a)(d-c))。勒贝格测度是数学上的一种方法,用于定义欧几里得空间的子集的长度、面积或体积。这种测度广泛应用于实分析,特别是在定义勒贝格积分时。
可以赋予一个体积的集合被称为勒贝格可测;勒贝格可测集A的体积或者说测度记作λ(A)。一个值为∞的勒贝格测度是可能的,但是即使如此,在假设选择公理成立时,R的所有子集也不都是勒贝格可测的。

在所定义的集合上,博雷尔测度与勒贝格测度是一致的;然而,仍然有更多勒贝格可测的集合不是博雷尔可测的。博雷尔测度是平移不变的,但不是完备的。哈尔测度可以定义在任何局部紧群上,是勒贝格测度的一个推广(带有加法的是一个局部紧群)。
豪斯多夫测度(参见豪斯多夫维数)是勒贝格测度的一个推广,对于测量的维数比n低的子集是很有用的,例如内的曲线或曲面,以及分形集合。不能把豪斯多夫测度与豪斯多夫维数的概念混淆。可以证明,在无穷维空间不存在勒贝格测度的类似物。

性质:
1、如果A是有限个或可数个两两互不相交的勒贝格可测集的并,那么A也是勒贝格可测的,并且λ(A)就是这些可测集的测度的和或无穷级数的和。
2、如果A勒贝格可测的,那么它的补集(相对于R)也是可测的。
3、对于每个勒贝格可测集A,λ(A)≥0 。
4、如果A与B是勒贝格可测的,且A是B的子集,那么λ(A)≤λ(B)。
5、可数多个是勒贝格可测集的交或者并仍然是勒贝格可测的。
博雷尔事件域为什么是可测的
区间,性质。1、区间:Rn中的区间(无论开闭)都是可测的。
2、性质:可测集对于可数并运算和余集运算封闭。正因为这条性质,从区间出发就可以构造多种可测集。
区间两端两个数能否相等?就如是否可写区间[1,1]?谢谢咯。
按区间[a,b]的定义,是要求a所以 [1,1],实际上是集合:{1}。
和数字“1” 还是有一点区别的。
在数学里
区间通常是指这样的一类实数集合:如果x和y是两个在集合里的数,那么,任何x和y之间的数也属于该集合。例如,由符合0 ≤ x ≤ 1的实数所构成的集合,便是一个区间,它包含了0、1,还有0和1之间的全体实数。其他例子包括:实数集,负实数组成的集合等。
区间在积分理论中起着重要作用,因为它们作为最"简单"的实数集合,可以轻易地给它们定义"长度"、或者说"测度"。然后,"测度"的概念可以拓,引申出博雷尔测度,以及勒贝格测度。
实变函数学习感悟
对实变函数的看法和感悟如下:一、实变函数课程内容简介
第一章主要简述了集合论,里面包含了集合的运算、基数、可数集等内容,以便更好地了解集合的性质。第二章则主要介绍了开集、闭集以及特殊的集合:Cantor集和Borel集。以此为基础第三章主要讲述了测度与外测度,有了可测集之后还有可测函数,第四章便主要讲述了可测函数。最后,便是最重要的还是Lebesgue积分。
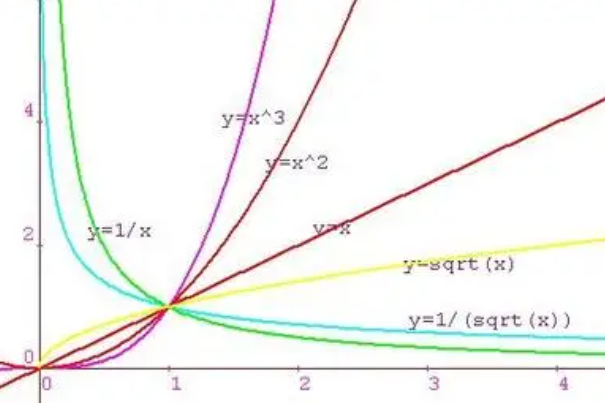
至于学习本课程所需预备知识,笔者认为需要数学分析的相关知识较多。主要是关于极限的一些内容,上极限、下极限、确界原理。以及黎曼积分和勒贝格积分之间的区别。
笔者认为本门课程和代数之间关联较少。而在学习的过程中发现概率论的基础是实变函数,而实变函数也因概率论的发展而被世人所重视。
二、本课程最艰难的部分,应该如何克服?
实变函数的难点在于有些定义较为抽象,比如勒贝格积分,博雷尔集类,不可测集、选择公理,这些定义、公理在理解上相对较为困难,难以想象,难以用某些东西去类比,因此相对其他学科会较为困难。而针对概念、定义上的困难,还是需要自己反复推敲才能较好地领悟其中奥妙。
因此,对于普通大学生来讲克服这些难点地关键在于自身,静下心思考,一遍、两遍、三遍,经过仔细琢磨,对这些知识点地理解也能更深入,难题也会迎刃而解。
而与其他学科相关地一些定义,如连续、上下极限、上下确界等内容相对较为容易理解,在学习实变函数时只需融会贯通,多加运用即可。
三、本课程最感兴趣的部份
比较吸引我的一点是实变函数与各学科的交集。实变与概率论、复变函数以及数学分析之间都有联系。从黎曼积分到勒贝格积分,我更希望看到勒贝格积分的具体内容,以及黎曼积分与勒贝格积分的具体差距。
